The Willow Tree Method, an Advanced Option Pricing Model
The Binomial tree is a standard method for pricing American style options. Recall that,
The Binomial options pricing model approach has been widely used since it is able to handle a variety of conditions for which other models cannot easily be applied. This is largely because the BOPM is based on the description of an underlying instrument over a period of time rather than a single point. As a consequence, it is used to value American options that are exercisable at any time in a given interval as well as Bermudan options that are exercisable at specific instances of time. Being relatively simple, the model is readily implementable in computer software (including a spreadsheet). Read more
Advantages of the Binomial method are its accuracy, simplicity, and the ability to handle the early exercise feature. However, the method also has disadvantages, notably,
For options with several sources of uncertainty (e.g., real options) and for options with complicated features (e.g., Asian options), binomial methods are less practical due to several difficulties, and Monte Carlo option models are commonly used instead. When simulating a small number of time steps Monte Carlo simulation will be more computationally time-consuming than BOPM (cf. Monte Carlo methods in finance). However, the worst-case runtime of BOPM will be O(2n), where n is the number of time steps in the simulation. Monte Carlo simulations will generally have a polynomial time complexity, and will be faster for large numbers of simulation steps. Monte Carlo simulations are also less susceptible to sampling errors, since binomial techniques use discrete time units. This becomes more true the smaller the discrete units become.
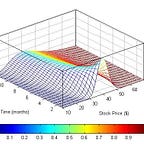
The “Willow” tree [1] is an advanced variant of the Binomial method that addresses the disadvantages of the latter.
… The Willow tree is constructed in a way that places nodes (and thus computation) in regions that are most important for general pricing problems. The Willow tree has been shown to be an extremely efficient improvement over such standard trees, and one that also provides the flexibility for a wide variety of processes and models.
The particular advantages of the Willow tree are vastly improved convergence of derivative prices and greeks, as well as superior stability. The Willow tree also gives complete freedom in choosing time steps, which simplifies the implementation of pricing models. Variations of the basic Willow tree model admit state-dependent volatilities in single- and multifactor models, and efficient and flexible computation of all types of barrier options.
This method was developed initially in 2001 for simple instruments and since then has been extended to more complex ones.
References
[1] M. Curran, Willow Power: Optimizing Derivative Pricing Trees, ALGO RESEARCH QUARTERLY, Vol. 4, №4, December 2001.
Article Source Here: The Willow Tree Method, an Advanced Option Pricing Model